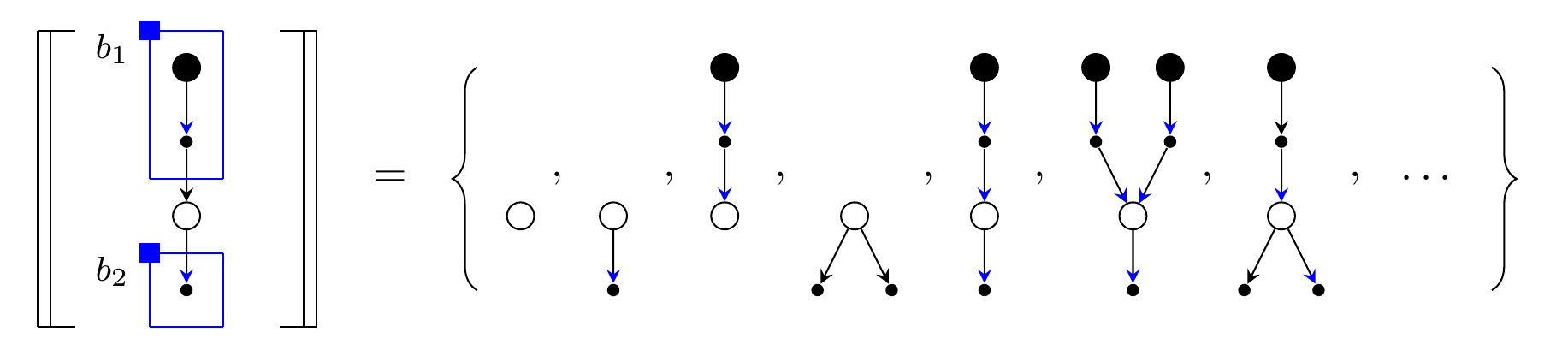
 Example !-box semantics
Example !-box semantics
Reasoning with !-graphs
Abstract
The aim of this thesis is to present an extension to the string graphs of Dixon, Duncan and Kissinger that allows the finite representation of certain infinite families of graphs and graph rewrite rules, and to demonstrate that a logic can be built on this to allow the formalisation of inductive proofs in the string diagrams of compact closed and traced symmetric monoidal categories. String diagrams provide an intuitive method for reasoning about monoidal categories. However, this does not negate the ability for those using them to make mistakes in proofs. To this end, there is a project (Quantomatic) to build a proof assistant for string diagrams, at least for those based on categories with a notion of trace. The development of string graphs has provided a combinatorial formalisation of string diagrams, laying the foundations for this project.
The prevalence of commutative Frobenius algebras (CFAs) in quantum information theory, a major application area of these diagrams, has led to the use of variable-arity nodes as a shorthand for normalised networks of Frobenius algebra morphisms, so-called “spider notation”. This notation greatly eases reasoning with CFAs, but string graphs are inadequate to properly encode this reasoning.
This dissertation extends string graphs to allow for variable-arity nodes to be represented at all, and then introduces !-box notation (and structures to encode it) to represent string graph equations containing repeated subgraphs, where the number of repetitions is abitrary. It then demonstrates how we can reason directly about !-graphs, viewed as (typically infinite) families of string graphs. Of particular note is the presentation of a form of graph-based induction, allowing the formal encoding of proofs that previously could only be represented as a mix of string diagrams and explanatory text.
This was my DPhil thesis. I worked in the Quantum Computer Science group at the University of Oxford. The big thing they do is develop a way of representing quantum processes as pictures that look like flow charts. The idea is that humans can more easily intuit what is going on - one of my supervisors called it “kindergarten quantum mechanics”.
The clever part is that you can manipulate these pictures according to certain straightforward rules, and this translates into mathematical proofs - they aren’t just an aid to understanding, they are mathematically rigourous.
My research focussed on developing techniques for doing (semi-)automated reasoning with these languages - in other words, getting a computer to both do some of the more tedious work of using the diagrams, and checking that your manipulations are correct. In particular, this thesis is on representing infinite families of rules in a finite way, so they can actually be used by a computer. There is a tool (Quantomatic) that implements this work.
This work was based on Aleks Kissinger’s thesis, and was continued by David Quick in his thesis.